
Share:
If a sample of size n is taken from a population that is Normally Distributed, the sampling distribution of the mean is also Normal. Even if the population is not Normal, as n increases – the sampling distribution of the mean tends to be a Normal Distribution.
Imagine, there is a village with 10,000 farmers. Each farmer takes a different amount of time to harvest their crops. So the harvest times vary a lot within the village.
We are curious about the overall pattern of harvest times among the farmers. To figure this out, we take a random group of 30 villagers. We measure the harvest time of each person in this group, calculate the average harvest time for that group, and record this average harvest time for the first group of 30 villagers.
Now, let’s do it again! We take another random group of 30 farmers, measure their harvest time, find the average harvest time for this second group, and record the average.
Remember that a farmer who was part of the first group could be randomly selected again for the next group (statistically, known as replacement).
We keep repeating this process, selecting different random groups of 30 villagers each time, measuring their harvest times, calculating their average, and recording this value.
After repeating this process many times, we have a bunch of average harvest times from various groups of 30 villagers.
The collection of all these average values is called Sampling Distribution.
Now, let’s look at all these recorded averages aka sampling distribution. We create a histogram or a bar chart that shows the frequency of each average harvest time value.
We observe that the distribution of average harvest times starts to look like a bell-shaped curve or a Normal Distribution.
In this bell-shaped curve, most of the average harvest times will gather around a central value (that’s how the word ‘central’ originated). This central value represents the average harvest time of the entire village.
As we move away from the central value on the bell curve, we find fewer average harvest times. This means that extreme values, either very long or very short harvest times, become increasingly rare as we move away from the average.
What’s really interesting is that this bell-shaped curve remains consistent, no matter how the individual harvest times were distributed within the village. Even if the harvest times were not originally following a normal pattern, the averages of these random groups still tend to follow this normal distribution.
And that’s the magic of the Central Limit Theorem! It tells us that as we take larger and larger samples from the population, calculate their averages, and repeat this process many times, the distribution of these averages will converge to a normal distribution.
The Central Limit Theorem is incredibly useful because it allows us to make predictions and draw conclusions about the entire village’s harvest times based on the averages of these random groups. It works even when the original data may be diverse or not normally distributed.
Now, let’s see this whole concept in action with the script below:
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(42) # You can use any integer value as the seed
# Define the population with exponential distribution - representing the harvest times of 10,000 individuals
population = np.random.exponential(scale=5, size=10000)
# The sample size is set to 30, which determines the number of individuals randomly selected from the population for each sample (remember CLT assumes a large sample ≥ 30)
sample_size = 30
'''
Sampling distribution: we draw samples of size 30 from the population (with replacement) and calculate the mean of each sample.
This process is repeated 1000 times, resulting in a list of 1000 sample means
'''
sample_means = [np.random.choice(population, sample_size, replace=True).mean() for _ in range(500)]
#=============================================================
# Check for Normaility: Visual Plots
#=============================================================
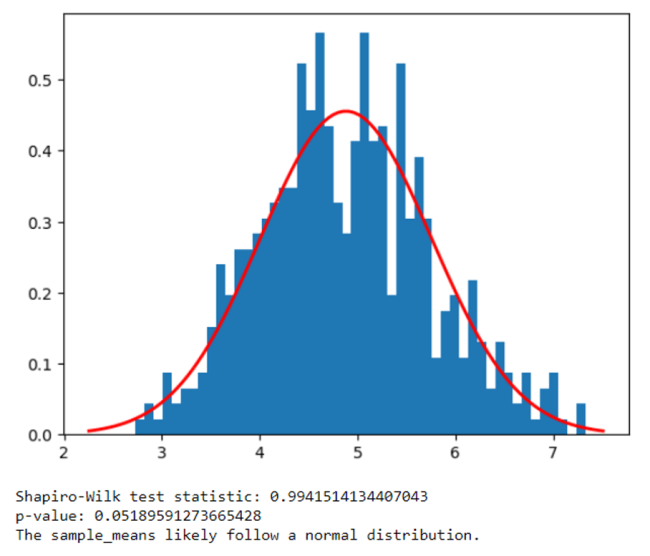
# Histogram plot of the sample means: We now visually check for the normality of the sample means using a histogram. We plot the histogram of the `sample_means` with 50 bins and sets the density parameter to True for a normalized distribution
plt.hist(sample_means, bins=50, density=True)
'''
Compare the histogram to a normal distribution: we calculate the mean and standard deviation of the `sample_means`.
We then generate a set of values, `x`, evenly spaced around the mean within three standard deviations.
This range is used to plot the probability density function (PDF) of the normal distribution.
Finally, it plots the normal distribution PDF on the same plot as the histogram, visualizing the comparison between the observed sample means and the expected normal distribution.
'''
mu = np.mean(sample_means)
sigma = np.std(sample_means)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.plot(x, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (x - mu)**2 / (2 * sigma**2) ), linewidth=2, color='r')
plt.show()
#=============================================================
# Check for Normaility: Shapiro-Wilk test
#=============================================================
# We now check for normality statistically using the Shapiro-Wilk test
statistic, p_value = stats.shapiro(sample_means)
# The test statistic measures the deviation from normality, while the p-value indicates the statistical significance
print(f"Shapiro-Wilk test statistic: {statistic}")
print(f"p-value: {p_value}")
'''
If the p-value is greater than alpha, it suggests that the sample means do follow a normal distribution.
Otherwise, it concludes that the sample means do not follow a normal distribution.
'''
alpha = 0.05 # Set the significance level
if p_value > alpha:
print("The sample_means likely follow a normal distribution.")
else:
print("The sample_means do not follow a normal distribution.")
Central Limit Theorem links to a general theory in Statistics:
If all possible random samples of size n are drawn with replacement from a population with mean µ and s.d. σ, then the means of the samples (called the sampling distribution of means) have a probability distribution with mean µ and s.d. σ⁄(√n) . This s.d. is known as std. error of means.
If the sampling is done without replacement i.e., no single farmer in multiple groups, then the std. error is given as:
std.\ err\ =\ \sqrt{\frac{\sigma^2}{n}\left(\frac{N-n}{N-1}\right)} where N is the population size.
Now whether the sampling is with or without replacement, std. error decreases as n increases. It is quite intuitive that, the larger the sample size n, the closer the sample mean to the population mean!
While the Central Limit Theorem (CLT) is a powerful statistical concept, it does have some limitations.
One of the assumptions of the CLT is that the sample size (n) should be sufficiently large, typically considered to be 30 or more. However, even with a sample size of 30 or more, there are situations where the sampling distribution may not exactly follow a perfect normal distribution.
The accuracy of the normal approximation in the sampling distribution depends on several factors, including the underlying distribution of the population, the sample size, and the amount of variability in the population.
Here are some scenarios where the sampling distribution may not follow a perfect normal distribution, even with a sample size of 30 or more:
1. Skewed Population: If the population itself has a highly skewed distribution, the sampling distribution may not become perfectly normal, especially if the sample size is relatively small.
2. Small Sample Size with Heavy Tails: In cases where the underlying population has heavy-tailed distributions (e.g., Cauchy distribution), the sampling distribution may still exhibit heavy tails, even with a sample size of 30.
3. Outliers: The presence of outliers in the population can impact the shape of the sampling distribution, especially if the outliers are present in multiple samples.
4. Bimodal or Multi-modal Population: If the population is bimodal or multi-modal, the sampling distribution may not be exactly normal.
Despite these limitations, the CLT remains a valuable concept in statistics as it provides a reliable way to make inferences about the population parameters using the sample means.
However, when working with smaller sample sizes or populations with non-normal distributions, it’s essential to be cautious and consider alternative methods for inference, such as non-parametric statistics or bootstrapping. These methods can provide more robust results in situations where the CLT assumptions may not hold.
Think about the sampling distribution – that bell curve.
A confidence interval in simple terms is a symmetric range in that bell curve that will contain the true population mean with a given confidence level.
Get the Sampling Distribution of the sample mean. You take multiple random samples of a certain size (n) from a population and calculate the sample means for each sample, those sample means will follow an approximately normal distribution. Your sampling distribution is ready!
Next, derive the two parameters: the mean (μ) and the standard error.
Define a confidence level (e.g., 95% confidence).
Find the critical values from the standard normal distribution (z-values) corresponding to your chosen confidence level. For a 95% confidence interval, the critical values are typically ±1.96.
Calculate the margin of error, which is the critical value multiplied by the standard error.
Construct the confidence interval by adding and subtracting the margin of error from the sample mean: (x̄ – margin of error, x̄ + margin of error).
The result is a confidence interval that provides a range of values within which we are reasonably confident (at the chosen confidence level) that the true population parameter lies.
For example, if we construct a 95% confidence interval for the population mean, it means that if we were to take many random samples and calculate confidence intervals in the same way, we would expect approximately 95% of those intervals to contain the true population mean.
Imagine you’re flipping a fair coin. If you only flip it a few times, you might get a result that’s quite different from a 50-50 split between heads and tails. For example, you could get 3 heads and 1 tail. But if you keep flipping the coin many, many times, the proportion of heads and tails will get closer and closer to 50-50. The more flips you do, the more likely your average result will match the expected 50% heads and 50% tails.
Hence, if you repeatedly flip the coin, the average of the outcomes (the proportion of heads and tails) will tend to approach 0.5 (the expected value for a fair coin) as the number of flips increases.
This is the concept of the Law of Large Numbers.
In simple terms, it states that as you repeatedly perform the same experiment or process many times, the average or expected value of your outcomes will get closer and closer to the true or theoretical average.
In essence, the Law of Large Numbers tells us that with a large enough sample size or a large number of trials, random fluctuations tend to even out, and the observed average converges toward the true or expected average.
It’s a fundamental principle in probability and statistics, and it underlies much of statistical analysis and inference.
The Central Limit Theorem (CLT) and the Law of Large Numbers (LLN) are two fundamental concepts in probability and statistics, but they have some differences.
Central Limit Theorem (CLT)
Law of Large Numbers (LLN)
In summary, the Central Limit Theorem deals with the distribution of sample means and how it becomes approximately normal as the sample size increases.
The Law of Large Numbers focuses on the behaviour of the sample mean itself and how it converges to the population mean as the sample size increases.
Both concepts are essential in statistical analysis and play crucial roles in making inferences and drawing conclusions based on data.
Central Limit Theorem & Law of Large Numbers

Question
Your answer:
Correct answer:
Your Answers
© 2023 DataScienzz. Powered by DataScienzz